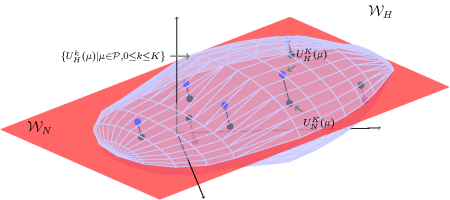
Background on Model Order Reduction
Proper Orthogonal Decomposition (POD)
Proper orthogonal decomposition (POD) provides a method for deriving low order models of dynamical systems. This approach is currently often used successfully as a model reduction technique for nonlinear PDEs, where the basis functions correspond to solutions of the dynamical system at pre-specified time-instances or parameter values, for a control that is selected by the user. These are called snapshots. Due to possible linear dependency or almost linear dependency, the snapshots themselves are not useful as a basis. Therefore, a singular value decomposition is carried out and the leading generalized eigenfunctions are chosen as a basis, referred to as the POD basis. Then, a POD-Galerkin approximation is applied in the spatial variable utilizing the POD basis functions as ansatz and test functions in the variational formulation of the PDE. POD was successfully used in a variety of fields including signal analysis and pattern recognition, fluid dynamics and coherent structures and inverse problems.
Reduced Basis (RB) Method
Reduced basis (RB) methods have been developed during the last decades with the aim to efficiently compute numerical solutions for parametrized applications. These are applications for which not only a single simulation has to be performed, but solutions for a range of different parameter configurations of the same problem are desired. This can be found in optimization, control, parameter estimation, statistical investigations or online-simulation settings. Realistic numerical discretization schemes result in huge numerical models which result in long computation times. Therefore, they are in general unsuitable for such real-time and many-query applications under parameter variation. Reduced basis methods provide a solution for reducing the dimensionality of such problems, giving efficient reduced simulation models, while simultaneously ensuring certified error statements for the simulation result.
Combined Reduction
Combined state and parameter reduction, or short combined reduction, addresses the swift solution of inverse problems on linear and nonlinear control systems with high dimensional state and parameter spaces. Two distinct approaches are explored in this model order reduction setting. Both methods assemble projections for state and parameter spaces to their respective dominant subspaces. First, empirical gramians are employed; especially the empirical cross gramian, as a tool for the concurrent computation of Petrov-Galerkin projections for state and parameters. Second, an iterative technique employing greedy sampling to assemble Galerkin projections for states and parameters. Either, the gramian-based and the optimization-based approach allow fast inference of the large-scale models which enables, an otherwise computationally infeasible, inversion of complex network models.
For More Information
For more information, we refer to the MOR-Wiki.